Un autómata finito o máquina de estado finito es un modelo matemático de un sistema que recibe una cadena constituida por símbolos de un alfabeto y determina si esa cadena pertenece al lenguaje que el autómata reconoce. Formalmente, un autómata finito (AF) puede ser descrito como una 5-tupla (S,Σ,T,s,A) donde: Ejemplo 1 Además de notar un AF a través de su definición formal es posible representarlo a través de otras notaciones que resultan más cómodas. Entre estas notaciones, las más usuales son: Ø υ 1* υ (1* ο 0 ο 1* ο 0)* Más información en: http://es.wikipedia.org/wiki/Aut%C3%B3mata_finito#Definici.C3.B3n_formal
Definición formal
 ;
; es el estado inicial;
es el estado inicial;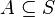 es un conjunto de estados de aceptación o finales.
es un conjunto de estados de aceptación o finales. Formas de representar un autómata finito
S1 S2 S1 S2 S1 S2 
Autómata finito
Suscribirse a:
Enviar comentarios (Atom)






No hay comentarios:
Publicar un comentario